Lesson 2 : Modelview & Projection transformations

•  Introduction

We have already see in the Tutorial 4 two transformation : translation and rotation.

The goal of these Lesson is to view the differents type of transformations. This lesson also show how to use it and how OpenGl store all these differentes transformations.

There are two kind of transformations :
    Modelview transformations (also called Modeling and Viewing transformation)
    Projection transfomations
 

•  Modelview transformations

Modelview transfomations are used to position the view in the scene.

•  glTranslate & glRotate

Translation and rotate are made with :
    glTranslate*(xTranslation, yTranslation, zTranslation)
    glRotate*(angle, xAxis, yAxis, zAxis)

(xAxis, yAxis, zAxis) is a unit vector defining the axis of rotation (ê on the picture below). It represents a unit vector. The angle parameter is the rotation angle in degree (θ on the picture).
This kind of rotation is commonly caled Euler axis-angle rotation.

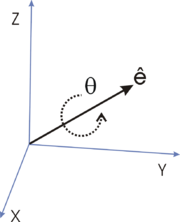
Axis/Angle rotation, picture from Wikipedia

You have to care about the order in which you call glTranslate and glRotate.
The importance of the order is shown on the two below pictures. In these pictures, the axis system is represented at each step.

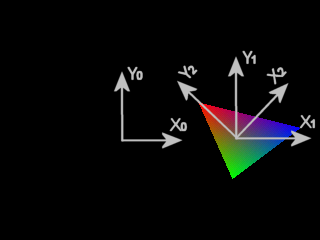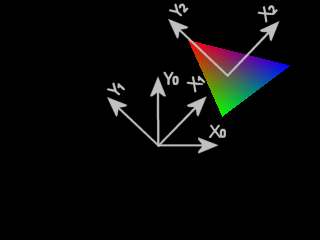Translation then rotation	Rotation then translation

Each transformations are sucessively applied to the current axis system.
The first call transformate the coordinate system from (X0, Y0) to (X1, Y1). The second call transformate the current coordinate system, which is now (X1, Y1), into (X2, Y2).
 

• glScale

There are a third transformation that scales the scene (resize the axis) :
    glScale*(xAxis, yAxis, zAxis)
The unit vector of each axis are multiplied by their corresponding parameter values of this method. Here is an exemple of scaling :

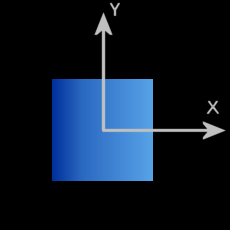glScale(-1.f, 0.5f, 1.f)

•  gluLookAt

To position ourself in a particular position in a scene, instead of calling glTranslate and glRotate many time, you can use gluLookAt :
    glu.gluLookAt(x, y, z,
        viewX, viewY, viewZ,
        topX, topY, topZ)
The point (x, y, z) is the view position.
The point (viewX, viewY, viewZ) is a point on the view direction.
The vector (topX, topY, topZ) is the vertical direction.
 

•  How OpenGl store these transformations

All these transformations can be represented by a 4 dimentional matrix :

A 4x4 matrix

Modelview transformations are stored in the Matrix Stack.
In OpenGl, the modelview matrix stack is represented by the matrix mode GL_MODELVIEW. It contains a stack of transformation push with glPushMatrix. Matrix on top of the GL_MODELVIEW matrix stack is the current transformation matrix.

To apply transformation (translation, rotation, scale), you should first select GL_MODELVIEW with :
    glMatrixMode(GL_MODELVIEW)
The default matrix mode is GL_MODELVIEW.

At the beginning, this matrix stack only contains the identity matrix (0 everywhere except on the diagonal m1/m16). The identity matrix is used to apply no transformations.
You can at any time reset the modelview transformation to the identity with :
    glLoadIdentity()

When a Modelview transformation is called, the current matrix (ie matrix on top of the stack) is multiplied by the matrix representation of the transformation. The current matrix is replaced by the resulting matrix.

Matrix representations are shown below :

Translation

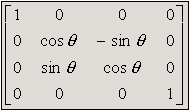
X rotation

Y rotation

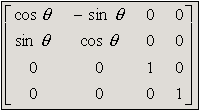
Z rotation

Scale

See the Matrix stack part to have more informations on matrix stack manipulation.
 

•  Projection transformations

The Lesson 1 tolds about Viewing Volume. This is a projection transformations.
Projection transformations defines how the 3D scene is projected in the 2D screen.

Projection transformations are stored in the matrix stack represented by GL_PROJECTION.
We select this Matrix mode using the same method seen in the previous transformation :
    glMatrixMode(GL_PROJECTION)

Perspective and orthographic projection is represented by the two following matrices :

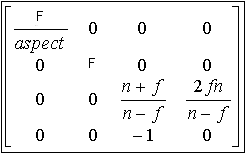
Perspective matrix
n = near, f = far and F = cotangent(fovy) = cos(fovy) / sin(fovy)

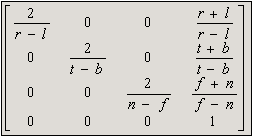
Orthographic matrix
n = near, f = far, r = right, l = left, t = top, b = bottom

•  Matrix stack

We have seen two matrix stack. There is a third matrix stack :
    GL_TEXTURE
This matrix mode will not be explained here.

Matrix stack is very usefull when we would creates hierarchical model (body, car ...).
The matrix stack can be used to do this :

•  save our current position (Modelview) or save the current viewing volume (Projection)

•  loads a previous position or a previous viewing volume

For saving the current current matrix, make a copy of the current matrix (matrix on top) and push it on top of the stack. This duplicate the current matrix. First matrix on top will be modified by subsequently transformations. Second matrix from the top will remains untouched.
This is done by the call :
    glPushMatrix()
Calling this method make a copy of the current matrix and put it on the top of the stack. Then, we have two identical matrix on the top of the stack.

The loading method is :
    glPopMatrix()
Calling this method delete/remove the matrix on top. The current matrix will be the second matrix of the stack before the deletion.
 

•  Use of glPushMatrix/glPopMatrix

A use of this can be view in Tutorial 7.

For modelview transformations, this can be used to save position of the coordinate system.
For projection transformations, this can be used to save the projection for switching between perspective (3D rendering) and orthographic (2D rendering : text ...). Switwhing between these two differents projections is used in Tutorial 17/20.
 

•  Manipulating matrices

You can use your own matrice to creates particular transformations.
To multiply the current matrix by your matrix :
    glMultMatrix(matrix)
matrix is a 16 length array which contains the 16 m_i value of the matrix represention.

You can also replace the current matrix by your own with :
    glLoadMatrix(matrix)
 

•  Offline reading

•  Matrix formulas (.xls)