![]()
![]()
In this lesson, we will see what is a Viewing Volume and
a Viewport. I think this is necessary to understand the Viewing Volume
to know how OpenGL works and draw a vertex from the *abstract* 3D space
to the window of the screen.
Some informations was found in the OpenGL Programming Guide also known
as The Red Book (html version here).
This book is really usefull,
I encourage you to read it !
The 3D space is defined by 3 axis
(vectors) : X, Y and Z. These 3 axis creates an axis system (see Tutorial 4 for a representation of this axis system).
All points of the 3D space can be expressed as a linear combination of these
vectors. A point is point represented by its coordinates (x, y, z), which means
x * X + y * Y + z * Z (upper case is a vector, low case is a scalar). The volume
of the entire 3D space is infinity.
The Viewing Volume delimites the 3D space by creating a closed volume.
Points outside this volume will not appears on the screen.
This particularity explain the first call glTranslate
(just after glLoadIdentity) : we go inside the Viewing Volume.
At start, we are on the front plane of the viewing volume.
The Viewing Volume can be created with two different kind of projections :
Perspective Projection
Render object affected by the distance, a car is seen smaller when it move away.
Orthographic Projection Render
object NOT affected by the distance like a menu, a text on the screen, 2D
objects ...
With this kind of projection, the viewing volume shape is a truncated pyramid (its top is
cutted).
This shape is abtained by 6 cutting planes : front, back, right, left, top and
bottom planes (planes at the volume boundary). These planes are commonly called Clipping Planes.
These planes can be created with the aid of the method :
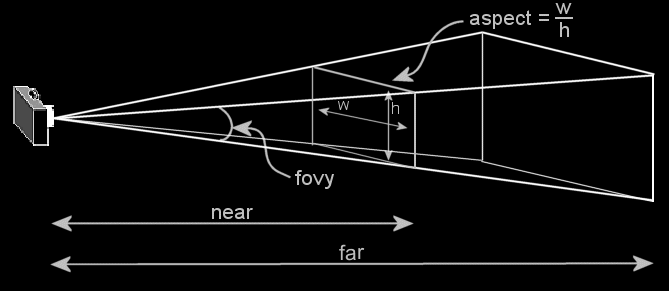
glu.gluPerspective(fovy, aspect, near, far)
The fovy parameter is the angle between the
plane that goes downwards and the plane that goes upwards.
The aspect ratio is generaly the aspect ratio
of the window (window is the region of the screen in which the scene is
rendered).
Each parameters are represented in this picture :
 |
Picture Copyrith @ Addison-Wesley Publishing Company |
The Viewing Volume looks like :
|
Viewing Volume obtained with gluPerspective |
The X and Y axis are parallel to the near plane. The origin of
the axis system is the center of the near plane. The Z axis is perpendicular to the near plane and points towards the view.
The call glLoadIdentity reset the axis system, like represented in the
above picture.
![]() Parameter
values
Parameter
values
Here is an exemple of a viewing volume with perspective projection :
gluPerspective(45.f, width/height, 1.f, 500.f)
The aspect parameter is the ratio between the width and the height of the
window (component holding the OpenGL scene).
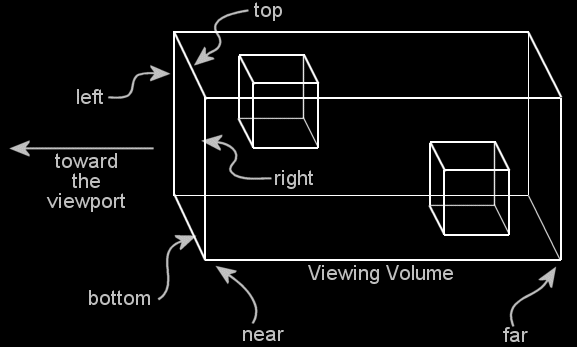
The Viewing Volume shape in this case is a parallelepiped. The 6
clipping planes delimiting the space can be created with the aid of :
gl.glOrtho(left, right, bottom, top, near, far)
Each parameters are represented in this picture :
 |
Picture Copyrith @ Addison-Wesley Publishing Company |
The viewing volume looks like :
 |
Viewing Volume obtained with glOrtho |
The axis system is represented in the above picture. In the
difference of the perspective projection, the origin is at the lower left corner
of the near plane, this means at the bottom left of the window.
![]() Values used
Values used
Here is an exemple of an orthographic projection :
gl.glOrtho(0, width, 0, height, -1, 1)
The width and height
are the dimension of the window.
Clipping planes can be used in addition of those used created
for the viewing volume. OpenGL define 6 clipping plane
GL_CLIP_PLANEi
(i goes from 0 to 5).
A clipping plane is a plane that separate the space in two regions. One region
is included from the viewing volume, the other is excluded.
In mathematics, a plane is defined by this equation :
a*x+b*y+c*z+d = 0
(x, y, z) are the coordinates of the points in the 3D space.
All points that verify this equation are on the plane.
The inequality (< or > instead of =) define the
region in each side of the plane.
In OpenGL, a clipping plane is the region defined by this equation :
a*x+b*y+c*z+d >= 0
A clipping plane is creates with the 4 values a, b, c & d likethis :
double[] eq = {a, b, c, d}
gl.glClipPlane(GL_CLIP_PLANEi, eq) //i can be 0, 1 ...
All points draw , the other are excluded (will not be rendered on the screen).
Like for lights, clipping planes have to be enable to be active :
gl.glEnable(GL_CLIP_PLANEi) //i can be 0, 1 ...
WARNING: The equation of the clipping plane is related to the axis system
at the time when glClipPlane was called (ie the clipping plane region is
affected by all previous glTranslate, glRotate and glScale calls). More
generally, the clipping plane is affected by the modelview matrix.
To find the plane equation, draw the axis system, the shapes to
be clipped and the clipping plane. Then, you pick-up four points on the plane and solve
the system of equations :
a*x1+b*y1+c*z1+d = 0
a*x2+b*y2+c*z2+d = 0
a*x3+b*y3+c*z3+d = 0
a*x4+b*y4+c*z4+d = 0
After a small headeach and few hour passed, you will find a, b, c and d
(a pocket calculator can be usefull).
The previous system of equations can be simplified to this
system with 3 equations / 3 unknwon variable :
a*x1+b*y1+c*z1+1 = 0
a*x2+b*y2+c*z2+1 = 0
a*x3+b*y3+c*z3+1 = 0
The system is now a little easier to resolve.
Effectively, the plane equition can be maniplated like this :
a*x + b*y + c*z + d = 0
is equivalent to (division by d) :
a/d*x + b/d*y + c/d*z + d/d = 0/d
The plane equation can be re-formulated as :
a'*x + b'*y + c'*z + 1=0
The values to send to OpenGl are now :
double[] eq = {a', b', c', 1}
An alternative is to used the method explained in
Tutorial 8.
Previously, we have seen how the viewing volume delimitate to 3D
space.
The Viewport is the region of the screen where this volume is projected.
The
viewport can be defined with :
gl.glViewport(x, y, width, height)
Tutorial 7 will show you how to use multiple viewport.
When the OpenGL window is reshape, those two properties are
updated to respect the new aspect ration and dimension of window.
For an undistored view, the aspect ratio of the viewing volume should be equals
to the aspect ratio of the viewport.
![]()
![]()
| Last modified on 01/07/2010 | |
| Copyright © 2004-2012 Jérôme JOUVIE - All rights reserved. | http://jerome.jouvie.free.fr/ |